Fórum studentů MFF UK

Oddělení B:

1. Zformulujte a dokažte větu o charakterizaci positivně defitních matic. (8 bodů)

2. Buď
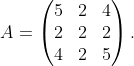
$A=\begin{pmatrix}5&2&4\\2&2&2\\4&2&5\end{pmatrix}.$
a) Najděte spektrální rozklad matice $A$ (4 body)
b) Aplikujte větu o deflaci dominantního vlastního čísla. (2 body)

3. Uvažujme kvadratickou formu $f(x)=x_1^2-2x_1x_2+4x_1x_3+3x^2_2+5x^2_3.$
a) Najděte matici formy vzhledem k bázi $(1,1,-1)^T,(-1,0,2)^T,(2,1,0)^T.$ (2 body)
b) Najděte věrohodným způsobem vektor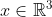 $x\in\mathbb{R}^3$ takový, že $f(x)<0$ . (4 body)

4. Rozhodněte a zdůvodněte, které z následujících tvrzení jsou pravdivé:
a) Pro každou čtvercovou matici $A$ platí $\det(A^TA)=\det(AA^T)$ . (2 body)
b) Jsou-li matice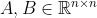 $A,B\in\mathbb{R}^{n\times n}$ diagonalizovatelné, pak i součin $AB$ je diagonalizovatelný. (2 body).
c) Matice $A$ je unitární
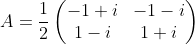$A=\frac{1}{2}\begin{pmatrix}-1+i&-1-i\\1-i&1+i\end{pmatrix}$ (2 body)
d) Pro každou matici $A$ platí rovnost sloupcových prostorů $\mathcal{S}(A^\dagger)=\mathcal{S}(A^T)$ (2 body)

Fórum studentů MFF UK

Hladík 8.6.2010

Hladík 8.6.2010