1) Uvedte platna tvrzeni:
a)
 = \Theta_\mathbb{P}(\Theta_\mathbb{P}(T)))
b)
 = \Theta_\mathbb{P}(T)\cap\Theta_\mathbb{P}(S))
b)
\subseteq\Theta_\mathbb{P}(S))
(Plati a), c) )
2) Budte
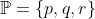
a teorie ve vyrokove logice
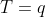
. Kolik je jednoduchych extenzi teorie T?
(
 = 2^2 = 4)
, S je jednoducha extenze T prave tehdy kdyz
 \subseteq M(T))
, tedy extensi je celkem jako podmnozin tridy modelu:
} = 2^4 = 16)
)
3) Necht mame
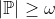
, tridu modelu
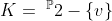
. Je
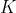
axiomatizovatelne?
(Sporem: K axiomatizovatelne, -K tez axiomatizovatelne skrze teorii
}| p\in\mathbb{P}\})
, tedy dle vety z prednasky je -K konecne axiomatizovatelne. Muzeme techto konecne axiomu spojit konjunkci do jedne formule, neboli
 = -K)
. To, zda-li je nejake pravdivostni ohodnoceni modelem teto teorie zalezi jen a pouze na prvovyrocich vyskytujicich se ve formuli

, zbytek lze volit libovolne. Ovsem zbyvajicicich prvovyroku je
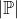
, tedy vsech moznych modelu teto teorie je
| = 2^{\mathbb{|P|}})
. Zaroven ovsem
| = |-K| = |\{v\}| = 1)
, coz je spor!)