Petr Glivický - SC0_U^{+-}

peci1 · Příspěvek od **peci1** » 31. 1. 2010 12:38

Ahoj, tady jsou moje návrhy (bez důkazů) na řešení našeho úkolu:

Má $SC0_U^\pm$ eliminaci kvantifikátorů? Ano
Je $SC0_U^\pm$ modelově kompletní? Ano, plyne z 1)
Popište všechny spočetné (až na izom.) modely $SC0_U^\pm$ , zjistěte $I(\omega,SC0_U^\pm)$ Je jich právě spočetně a jsou to modely SC takové, že 0 nemá předchůdce a ke každému přidám buď U(0) nebo 'U(0).
Zjistěte izomorfní spektrum a spektrum modelů $SC0_U^\pm$ ; $I(\omega,SC0_U^\pm) = \omega$ , jinak je rovno 0; $M(\omega, SC0_U^\pm) = 2^\omega$ , jinak je rovno 0
Najděte všechny jednoduché kompletní extenze $SC0_U^\pm$ . Je $SCO_U^\pm$ kompletní? Je kompletní, je tedy sama sobě jednoduchou kompletní extenzí
Je $SC0_U^\pm$ rozhodnutelná? Ano
Má $SC0_U^\pm$ prvomodel (algebraický prvomodel)? Algebraický prvomodel ano, prvomodel nevím
Je $SC0_U^\pm$ otevřeně axiomatizovatelná? Je konečně axiomatizovatelná? Ani jedno

Požádal jsem mailem Mgr. Glivického, aby se k těmto výsledkům na fóru vyjádřil, tak si můžete počkat.

PGlivicky · Příspěvek od **PGlivicky** » 1. 2. 2010 15:24

Zdravím. Níže jsou moje připomínky k jednotlivým odpovědím.

1) Nemá. Uvažujte modely $B = \langle N,0^N,S^N,U^B\rangle$ a $A = \langleN\dot{\cup}Z,0^N,S^N\dot{\cup}S^\Z,U^A\rangle$ , kde $U^A=N=U^B$ a zobrazení $f:0^A\mapsto0^B$ . $f$ je parciální vnoření, ale není splněna podmínka 1-koexistence (najděte vhodnou 1-primitivní formuli, která to prokazuje).

2) Nemá. Lze ověřit téměř stejně jako v 1).

3) Izomorfní spektrum v $\omega$ je správně. Jinak ale bych tady chtěl skutečně přesný popis (viz např. materiál Teorie a jejich analýza z http://kti.ms.mff.cuni.cz/~mlcek/index.html , kde je taková charakterizace podána v důkazu tvrzení 1.3.5.2. -- zejména v (1.8.)). Určitě nestačí rozlišit modely SC tím, zda platí U v 0 či ne - viz opět modely A,B z 1), které jsou neizomorfní, spočetné a přitom v obou platí U(0).

4) $I(\omega,SC0_U^\pm)$ = \omega je správně. Dále je pravda, že $I(n,SC0_U^\pm) = 0$ pro n konečné. Ovšem jistě je nenulové pro $\kappa>\omega$. Konkrétní hodnotu lze vyjádřit pomocí počtu kardinálů menších než jistá mez (není nutné zapisovat formálně množinově teoreticky - $|\lambda \cap Cn|$ ; stačí slovně).

5) Kompletní není. Například není dokazatelné U(0) ani $eg U(0)$ . Podobně nelze dokázat ani vyvrátit tvrzení typu "U(x) pro každé [nějaké] x", "pro nějaká x,y platí U(x) a $eg U(y)$ ". Správným kombinováním těchto nezávislých tvrzení lze vytvořit všechny jednoduché kompletní extenze.

6) Ano. Teď to jen správně zdůvodnit.

7) Algebraický prvomodel nemá. Např. modely A,B, kde U platí v 0 v A a neplatí v 0 v B, nemají společnou podstrukturu. Z toho již neexistence algebraického prvomodelu snadno plyne.

8 ) Správně.

Pro získání zápočtu není bezpodmínečně nutné mít vyřešeno všech 8 bodů, stačí že bude většina z nich alespoň v hrubých obrysech správně. Netrapte se tedy, zbytečně, kdybyste si nevěděli rady s jedním z bodů a ostatní jste měli již vzorově vyřešeno.

Petr Glivický

peci1 · Příspěvek od **peci1** » 6. 2. 2010 16:38

Ahoj, můj návrh na řešení a). Nejsem si úplně jistej tím závěrem s eliminační množinou.

a) Má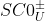 $SC0_U^{\pm}$ eliminaci kvantifikátorů? Pokud ne, jaká je její eliminační množina?
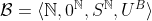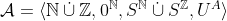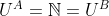Nemá. Budeme uvažovat modely $\mathcal{B} = \langle \mathbb{N}, 0^\mathbb{N}, S^\mathbb{N}, U^B \rangle$ a $\mathcal{A} = \langle \mathbb{N} \mathbin{\dot{\cup}} \mathbb{Z}, 0^\mathbb{N}, S^\mathbb{N} \mathbin{\dot{\cup}} S^\mathbb{Z}, U^A \rangle$ , kde $U^A = \mathbb{N} = U^B$ .

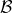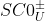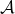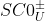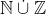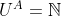$\mathcal{B}$ je model $SC0_U^{\pm}$ zřejmě. Ukážeme, že i $\mathcal{A}$ je modelem $SC0_U^{\pm}$ . Můžeme si pro názornost rozepsat $\mathbb{N} \mathbin{\dot{\cup}} \mathbb{Z}$ jako $\lbrace (1,\mathbb{N}), (2,\mathbb{N}), (3,\mathbb{N}), \dots, (-2,\mathbb{Z}), (-1,\mathbb{Z}), (0,\mathbb{Z}), (1,\mathbb{Z}), (2,\mathbb{Z}), \dots \rbrace$ . Víme, že $U^A = \mathbb{N}$ . Z přidaných axiomů by se mohlo zdát, že vynucují, aby U platilo buď pro celé univerzum, nebo pro žádný prvek. Ukážeme ale, že tomu tak není. 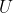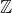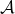Z axiomu $U(x) \rightarrow U(Sx)$ a toho, že $S(x,\mathbb{N}) = (x+1, \mathbb{N})$ vidíme, že tento axiom nevynucuje platnost $U$ o nějakém prvku $\mathbb{Z}$ v $\mathcal{A}$ . Stejně tak i axiom $U(Sx) \rightarrow U(x)$ . 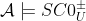Tedy i $\mathcal{A} \models SC0_U^{\pm}$ .

Atomické $L$ -formule mohou být následující:

$S^nx=y$ (první 4 jsou shodné s atomickýmiL-formulemi $SC0$ )
$S^nx=0$
$S^n0=y$
$S^n0=0$
$U(S^nx)$ (protože každý $\langle S,0 \rangle$ -term je v $SC0$ roven termu $S^nx$ nebo $S^n0$ a jazyk $\langle S, U\rangle$ přidává jen jeden predikátový symbol - a ten se v termech nevyskytuje)
$U(S^n0)$

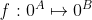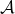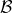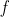Ukážeme, že $\mathit{f}:0^A \mapsto 0^B$ je \emph{parciální vnoření $\mathcal{A}$ do $\mathcal{B}$ }. Potřebujeme tedy, aby pro každou atomickou formuli $\varphi(\overline{x})$ (viz seznam výše) platilo $\mathcal{A} \models \varphi[\overline{a}] \Leftrightarrow \mathcal{B} \models \varphi[f\overline{a}]$ , kde $\overline{a} \in dom(\mathit{f})^{lh(\overline{x})}$ . 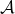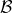Ale $\mathit{f}$ pouze zobrazuje $0$ z $\mathcal{A}$ na $0$ z $\mathcal{B}$ a ostatní realizace zachovává. Tedy 1) a 5) požadovanou podmínku splňují. Ostatní atomické formule podmínku také splňují, neboť 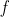$\mathit{f}$ nám právě zařídí, aby se zachoval význam $0$ v obou modelech (tj. $0$ nemá předchůdce). 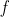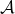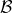Tedy $\mathit{f}$ je parciální vnoření $\mathcal{A}$ do $\mathcal{B}$ .

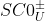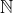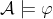Teď ukážeme, že $SC0_U^{\pm}$ není 1-koexistenční. Definujme formuli $\varphi(x) = (\exists y) ( eg U(y) \& U(x))$ . Ta je zjevně \emph{1-primitivní}. $\mathcal{B} ot\models \varphi$ , protože $U(x)[\mathit{f}(0^\mathcal{A}) = 0^\mathcal{B}]$ platí (protože 0 je realizována do $\mathbb{N}$ , tedy univerza, a U platí pro celé univerzum) a neexistuje $c$ , že $eg U(y)[c]$ . 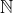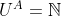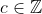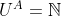Ale $\mathcal{A} \models \varphi$ , protože $U(x)[0^\mathcal{B}]$ platí (protože 0 je realizována do $\mathbb{N}$ a $U^A = \mathbb{N}$ ) a pro libovolné $c \in \mathbb{Z}$ máme $eg U(y)[c]$ (protože $U^A = \mathbb{N}$ , a tedy $-U^A = (\mathbb{N} \mathbin{\dot{\cup}} \mathbb{Z}) \setminus \mathbb{N} = \mathbb{Z}$ ). 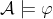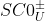Máme $\mathcal{B} ot\models \varphi$ , $\mathcal{A} \models \varphi$ a $\varphi$ 1-primitivní, a tedy $SC0_U^{\pm}$ není 1-koexistenční.

Podle 5.2.5 1)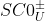 $SC0_U^{\pm}$ nemá eliminaci kvantifikátorů.

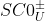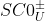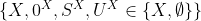Budeme tedy hledat eliminační množinu $SC0_U^{\pm}$ . Extenze $SC0_U^{\pm}$ o axiom $eg (\exists x)(\exists y)(U(x) \wedge eg U(y))$ má eliminaci kvantifikátorů (pak totiž všechny modely mají tvar $\lbrace X, 0^X, S^X, U^X \in \{X, \emptyset\} \rbrace$ a tím pádem každé neprázdné parciální vnoření mezi dvěma modely se dá bezprostředně prodloužit). Tedy eliminační množina 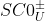$SC0_U^{\pm}$ je $AFm \cup \{ eg (\exists x)(\exists y)(U(x) \wedge eg U(y))\}$ .

blabla · Příspěvek od **blabla** » 11. 2. 2010 13:40

fuu no neviem mozno som blby, ale nechapem co ma znamenat toto ze N zjednotenie Z = { (1,N),(2,N),.....,(-2,Z),(-1,Z),(0,Z),(1,Z),......}...zjednotenie N a Z by podla mna logicky mal byt Z nie? ale mozno je moja logika slaba:D

peci1 · Příspěvek od **peci1** » 11. 2. 2010 17:14

blabla píše:fuu no neviem mozno som blby, ale nechapem co ma znamenat toto ze N zjednotenie Z = { (1,N),(2,N),.....,(-2,Z),(-1,Z),(0,Z),(1,Z),......}...zjednotenie N a Z by podla mna logicky mal byt Z nie? ale mozno je moja logika slaba:D

Doufal jsem, ze kdyz si nekdo te tecky nad sjednocenim nevsimne, tak mu prave ta prava strana prijde divna a casem tu tecku objevi. V podstate neni treba vedet, co ten operator dela, staci jen vedet, ze vysledek vypada takhle

Pro zajimavost je to neco jako "disjunktni sjednoceni" (viz http://en.wikipedia.org/wiki/Disjoint_union ) - sam jsem to nevedel, musel jsem to hledat asi pul hodiny po netu (zacal jsem tim, ze jsem dal citovat odpoved p. Glivickeho a v LaTeXu videl \dot\cup ). Mam ale takovy pocit, ze to neni poprve, co jsem se s tim operatorem setkal, dokonce mam neblahy pocit, ze dokonce na cviceni z logiky, ale ma pamet je temna =)

blabla · Příspěvek od **blabla** » 12. 2. 2010 18:13

nasiel som forum kde asi nejakej spoluziacke niekto vysvetloval tento prikld, nakoniec dostala zapocet takze zrejme tam najdete spravne odpovede, ak ste o tom nevedeli tu je link
http://forum.matweb.cz/viewtopic.php?pid=96336

matejcik · Příspěvek od **matejcik** » 18. 2. 2010 20:46

přikládám moje řešení, zpracované s použitím materiálů tady i tam - odpověď "Neni to dobre uplne vsechno, ale na zapocet to staci."
(kdybyste někdo dokázal vysvětlit, co je tam špatně a proč, bylo by to fajn.)

Fórum studentů MFF UK

Petr Glivický - SC0_U^{+-}

Petr Glivický - SC0_U^{+-}

Re: Petr Glivický - SC0_U^{+-}

Re: Petr Glivický - SC0_U^{+-}

Re: Petr Glivický - SC0_U^{+-}

Re: Petr Glivický - SC0_U^{+-}

Re: Petr Glivický - SC0_U^{+-}

Re: Petr Glivický - SC0_U^{+-}