Ahoj,
nevi nekdo z prezencnich studentu, co chodili na cviceni, jak sestrojit ten aproximacni algoritmus pro BTSP? Reseni jsem nasel jenom v jedinych zapiscich ve studnici ale nedokazu to z toho pochopit.
Hlavne nevim, co je to T^3, proc je zrejme, ze ma HK a jakou roli tam hraje ta trojuhelnikova nerovnost.
Snad se najde jeste nekdo, kdo cte fora vecer pred zkouskou (ja jdu jeste jen na zapocet)
Diky!
Bottleneck TSP
-
Krakonoš
- Matfyz(ák|ačka) level I
- Příspěvky: 14
- Registrován: 29. 1. 2009 11:31
- Typ studia: Informatika Mgr.
- Login do SIS: 84250710
Re: Bottleneck TSP
Ahoj,
takže já nejsem poctivý student, na cvičení nechodím, a když jsem se to pokusil najít, tak to nikde není pořádně napsané. Takže zhruba na co jsem přišel (termín kratší je vzhledem k metrice, lehčí/těžší k váhové funkci):
Je dobré vědět, že každá hamiltonovská kružnice je alespoň tak těžká, jako minimální kostra (vynecháním libovolné hrany z HK mám kostru, tím jsem si ale mohl pouze odlehčit).
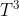 je graf, který vznikne z kostry přidáním zkratek (dál kdykoliv mluvím o zkratce, tak myslím takovouto hranu), které překročí nanejvýš 3 hrany.
je graf, který vznikne z kostry přidáním zkratek (dál kdykoliv mluvím o zkratce, tak myslím takovouto hranu), které překročí nanejvýš 3 hrany.
Také by mělo být jednoduché ubastlit nějaký algoritmus, který ti najde v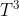 HK -- podobně jako u normální redukce TSP, prostě procházíš strom a když narazíš na navštívený vrchol, tak ho přeskočíš, jenom je potřeba být trošku opatrnější, protože nemůžeš skákat neomezeně daleko. Podle mě stačí nějaký hloupý algoritmus, který jde DFS a vždy jeden vrchol vynechá, když se vrací tak jde po těch vynechaných vrcholech a skoky délky 3 si nechá na případ, když je někde nějaká blbá kombinace liché/sudé cesty (asi by to šlo zformulovat lépe, ale hlavní je myšlenka).
HK -- podobně jako u normální redukce TSP, prostě procházíš strom a když narazíš na navštívený vrchol, tak ho přeskočíš, jenom je potřeba být trošku opatrnější, protože nemůžeš skákat neomezeně daleko. Podle mě stačí nějaký hloupý algoritmus, který jde DFS a vždy jeden vrchol vynechá, když se vrací tak jde po těch vynechaných vrcholech a skoky délky 3 si nechá na případ, když je někde nějaká blbá kombinace liché/sudé cesty (asi by to šlo zformulovat lépe, ale hlavní je myšlenka).
Teď nám jenom stačí ukázat, že není ta HK moc špatná. To je ale jednoduché. Kdybychom šli pouze po kostře, tak je všechno OK. Ale my jsme brali zkratky -- každou teoreticky až přes 3 hrany. Kdyby váha zkratky byla nanejvýš 3-krát větší než váha cesty, jsme v suchu (chyba se nesčítá přes všechny zkratky, je to maximum!). Kdyby ale byla váha ostře větší než 3-krát, tak délka cesty je nanejvýš délka zkratky (ostře) a neplatí trojúhelníková nerovnost (vyplatilo by se jít po třech hranách namísto jedné...). Tedy jsme si každou zkratkou pohoršili nanejvýš 3-krát a celkové to samé (opakuji, že chyba se nekumuluje, je to maximumové váhová funkce). Hurá.
(Protože všechny poznámky co mám jsou zmatené, nečitelné, nebo obojí, tak nedávám žádnou záruku. Pevně ale věřím tomu, že to funguje. Navíc asi existuje jednodušší algoritmus na nalezení HK (snáz dokazatelný), ale v jednu v noci to po mě nikdo nemůže chtít )
)
Zdar odpoledne na zápočtové písemce
takže já nejsem poctivý student, na cvičení nechodím, a když jsem se to pokusil najít, tak to nikde není pořádně napsané. Takže zhruba na co jsem přišel (termín kratší je vzhledem k metrice, lehčí/těžší k váhové funkci):
Je dobré vědět, že každá hamiltonovská kružnice je alespoň tak těžká, jako minimální kostra (vynecháním libovolné hrany z HK mám kostru, tím jsem si ale mohl pouze odlehčit).
Také by mělo být jednoduché ubastlit nějaký algoritmus, který ti najde v
Teď nám jenom stačí ukázat, že není ta HK moc špatná. To je ale jednoduché. Kdybychom šli pouze po kostře, tak je všechno OK. Ale my jsme brali zkratky -- každou teoreticky až přes 3 hrany. Kdyby váha zkratky byla nanejvýš 3-krát větší než váha cesty, jsme v suchu (chyba se nesčítá přes všechny zkratky, je to maximum!). Kdyby ale byla váha ostře větší než 3-krát, tak délka cesty je nanejvýš délka zkratky (ostře) a neplatí trojúhelníková nerovnost (vyplatilo by se jít po třech hranách namísto jedné...). Tedy jsme si každou zkratkou pohoršili nanejvýš 3-krát a celkové to samé (opakuji, že chyba se nekumuluje, je to maximumové váhová funkce). Hurá.
(Protože všechny poznámky co mám jsou zmatené, nečitelné, nebo obojí, tak nedávám žádnou záruku. Pevně ale věřím tomu, že to funguje. Navíc asi existuje jednodušší algoritmus na nalezení HK (snáz dokazatelný), ale v jednu v noci to po mě nikdo nemůže chtít
Zdar odpoledne na zápočtové písemce
-
Krakonoš
- Matfyz(ák|ačka) level I
- Příspěvky: 14
- Registrován: 29. 1. 2009 11:31
- Typ studia: Informatika Mgr.
- Login do SIS: 84250710
Re: Bottleneck TSP
Ahoj,
tak už jsem také zjistil algoritmus od Čepka na konstrukci HK: Indukcí podle počtu vrcholů dokazuji, že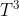 má HK obsahující předepsanou hranu
má HK obsahující předepsanou hranu  . Pro trojúhelník je to triviální. Jinak: Zvolím libovolnou hranu, rozdělím vrcholy na dvě části tak, aby každá obahovala jeden z vrcholů dané hrany (říkejme jim hraniční vrcholy). Zvolím pro každou část nějakou hranu incidentní s hraničním vrcholem, pustím indukci a mám dvě HK spojené hranou. Protože ale je to
. Pro trojúhelník je to triviální. Jinak: Zvolím libovolnou hranu, rozdělím vrcholy na dvě části tak, aby každá obahovala jeden z vrcholů dané hrany (říkejme jim hraniční vrcholy). Zvolím pro každou část nějakou hranu incidentní s hraničním vrcholem, pustím indukci a mám dvě HK spojené hranou. Protože ale je to 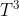 , lze ty HK spojit vhodnou zkratkou (pokud nevíte jak, namalujte si obrázek
, lze ty HK spojit vhodnou zkratkou (pokud nevíte jak, namalujte si obrázek  ).
).
tak už jsem také zjistil algoritmus od Čepka na konstrukci HK: Indukcí podle počtu vrcholů dokazuji, že
-
vojta_vorel
- Matfyz(ák|ačka) level I
- Příspěvky: 49
- Registrován: 14. 1. 2011 15:10
- Typ studia: Informatika Ph.D.
- Login do SIS: 35685873
Re: Bottleneck TSP
Je potřeba tu kružnici v T^3 hledat? Vím, že tam nějaká je, a to přeci pro 3-aproximaci stačí (vím, že optimum je větší než váha T, takže když algoritmus nechám vyplivnout tojnásobek váhy T... je hotovo).Také by mělo být jednoduché ubastlit nějaký algoritmus, který ti najde v T^3 HK
Vojta
EDIT: Ok, asi by se měla najít, na přednáškách se v takových případech pod "aproximací" problému typu "najdi nejmenší..." myslívalo "nalezení suboptimálního řešení a vrácení suboptima". Ale mate mě, že nám na cviku snad ani nezdůrazňovali že by se tohle dohledání mělo odehrát. Ačkoliv tedy to proskákávání zkratkovitým stromem asi nic složitého nebude...
No, jestli v tom někdo má úplně jasno, tak sem s tím. Trochu jsem se teď celkově zamotal v tom, jestli "rozhodnut o existenci" může být lehčí než "najít"...