Oproti loňským letům díky lehké reorganizaci zmizelo pár příkladů řešených na cvičení a oproti tomu přibyla hromada jiných. Nemáte hinty jak na ně?
5. cvičení
1.Nechť máme k dispozici „černou skřínku“, která umí řešit rozhodovací verzi problému součtu podmnožiny v polynomiálním čase. Skřínka odpovídá pouze ANO-NE. Zkonstruujte algoritmus, který pro daný vstup optimalizační verze problému součtu podmnožiny najde v polynomiálním čase (vzhledem k délce binárního zápisu vstupních dat) optimální řešení.
2.Popište jak lze pro libovolné dané n zkonstruovat graf na n vrcholech takový, že aproximační algoritmus pro vrcholové pokrytí s poměrovou chybou r=2 (prezentovaný na přednášce) na tomto grafu vrací pokrytí právě dvakrát větší než je velikost optimálního vrcholového pokrytí (tj. ukažte, že dokázaný odhad poměrové chyby je těsný).
3.Navrhněte algoritmus, který v polynomiálním čase nalezne optimální vrcholové pokrytí pro neorientovaný graf bez cyklů (les, strom).
4.Bottleneck TSP: vstupem je úplný ohodnocený neorientovaný graf s nezápornými váhami na hranách (stejně jako u obyčejného TSP), o kterých navíc předpokládáme, že splňují trojúhelníkovou nerovnost. Úkolem je opět najít nejkratší Hamiltonovskou kružnici ve vstupním grafu, ovšem délka kružnice není v tomto případě rovna součtu délek hran na kružnici, ale maximu z délek hran na kružnici. Nejdříve dokažte, že Bottleneck TSP je NP-těžký a poté navrhněte polynomiální aproximační algoritmus s poměrovou chybou r=3.
Nové příklady na cvičení
- tutchek
- Site Admin
- Příspěvky: 795
- Registrován: 21. 9. 2004 00:40
- Typ studia: Informatika Mgr.
- Login do SIS: tulam4am
- Bydliště: Praha, Bohnice
- Kontaktovat uživatele:
Nové příklady na cvičení
exAdmin. Magistr přes umělou inteligenci. Právník přes daně.
- macbeth
- Matfyz(ák|ačka) level III
- Příspěvky: 201
- Registrován: 11. 2. 2005 14:48
- Typ studia: Informatika Mgr.
- Bydliště: PPraha
- Kontaktovat uživatele:
Re: Nové příklady na cvičení
1.)suma xi <= t, black box nam povie ano, ak existuje Si: suma xi cez prvky Si = t
ide tam o pridavanie y0 = 20, y1 = 21, ... ylog_2 t = 2log_2 t (tie log s dolnou celou castou), potom nasu instanciu tvoria xj, yi a t a pytame sa, ci sa da t poskladat z yi... presne som to nepochopil, doplnte ma niekto...
2.) hviezda -- jeden vrchol v strede spojeny so vsetkymi vrcholmi usporiadanymi do kruhu okolo stredu... algoritmus vyberie nahodnu hranu a odstrani jej 2 vrcholy... pritom optimalne VP je tvorene len tym stredom... alebo nejaka modifikacia grafu tvoreneho dvojicami vrcholov spojenymi hranou, cosi ako
len tam treba vymysliet co s neparnym poctom...
3.) ideme od listov, tie neofarbime, ale ofarbime ich rodicov, potom odstranim hrany veduce medzi listami a ich rodicmi aj s danymi vrcholmi a iterujem... ofarbene vrcholy by mali byt potom VP... spravnost sa da dokazat podobne ako spravnost algoritmu B na prednaske, hrany su po 2 disjunktne, vybrana nemoze byt incidentna s inou potom...
hadam ma ostatni doplnia...
ide tam o pridavanie y0 = 20, y1 = 21, ... ylog_2 t = 2log_2 t (tie log s dolnou celou castou), potom nasu instanciu tvoria xj, yi a t a pytame sa, ci sa da t poskladat z yi... presne som to nepochopil, doplnte ma niekto...
2.) hviezda -- jeden vrchol v strede spojeny so vsetkymi vrcholmi usporiadanymi do kruhu okolo stredu... algoritmus vyberie nahodnu hranu a odstrani jej 2 vrcholy... pritom optimalne VP je tvorene len tym stredom... alebo nejaka modifikacia grafu tvoreneho dvojicami vrcholov spojenymi hranou, cosi ako
Kód: Vybrat vše
o o o o
| | | |
| | | | ...
o o o o
3.) ideme od listov, tie neofarbime, ale ofarbime ich rodicov, potom odstranim hrany veduce medzi listami a ich rodicmi aj s danymi vrcholmi a iterujem... ofarbene vrcholy by mali byt potom VP... spravnost sa da dokazat podobne ako spravnost algoritmu B na prednaske, hrany su po 2 disjunktne, vybrana nemoze byt incidentna s inou potom...
hadam ma ostatni doplnia...
Nieco, co by nejavilo ziadne znamky bytia, teda by sa nijak neprejavovalo ako sucno, by nebolo niecim, ale prave nicim...
- Blaf
- Matfyz(ák|ačka) level I
- Příspěvky: 12
- Registrován: 28. 1. 2008 12:13
- Typ studia: Informatika Bc.
Re: Nové příklady na cvičení
4) BottleneckTSP
prevod HK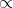 BTSP skoro stejnej, jako u normalniho TSP: nehrany ohodnotim 2, hrany 1 a ptam se, jestli existuje kruznice vahy 1. Aproximacni algoritmus se zase dela pres min. kostru, vyuziju fakt, ze "G je souvisly
BTSP skoro stejnej, jako u normalniho TSP: nehrany ohodnotim 2, hrany 1 a ptam se, jestli existuje kruznice vahy 1. Aproximacni algoritmus se zase dela pres min. kostru, vyuziju fakt, ze "G je souvisly 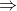 G3 je hamiltonovsky" a z trojuhelnikovy nerovnosti pak plyne, ze kruznice nebude delsi, nez trojnasobek minimalni kostry.
G3 je hamiltonovsky" a z trojuhelnikovy nerovnosti pak plyne, ze kruznice nebude delsi, nez trojnasobek minimalni kostry.
prevod HK