1. Definujte pojem báze. Zformulujte a dokažte větu o existenci báze.
2. Buď
$$B=\left(\begin{array}{ccc}1 & 2 & 1\\2 & -1 & 7\\1 & 1 & 2\\3 & 2 & 7\end{array}\right))
Rozhodněte, zda
=S(B))
.
Rozhodněte, zda
=S(A))
.
3. Uvažujme dvě lineární zobrazí
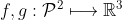
zadaná
=\left(11,1,4\right)^{T}\\f\left(x^{2}+4x+2\right)=\left(3,5,-2\right)^{T}\\f\left(3x^{2}+3x+2\right)=\left(1,0,2\right)^{T}\end{array}\begin{array}{c}g\left(x^{2}\right)=\left(1,-2,2\right)^{T}\\g\left(x\right)=\left(-2,0,1\right)^{T}\\g\left(1\right)=\left(1,2,-1\right)^{T}\end{array})
Zvolte si bázi

prostoru
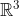
a spočítejte matici
![_{kan}\left[g\circ f^{-1}\right]_{B}](http://latex.codecogs.com/gif.latex?_{kan}\left[g\circ f^{-1}\right]_{B})
.
Rozhodněte, zda
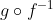
zobrazuje lineárně nezávislou množinu vždy zase na lineárně nezávislou.
4. Rozhodněte a zdůvodněte, která z následujících tvrzení jsou pravdivá:
(a) Buď

dolní trojúhelníková matice. Pak
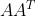
je zase dolní trojúhelníková matice.
(b) Každou permutaci na

prvcích lze zapsat jako složení
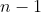
transpozic.
(c) Buď
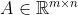
. Pak
=n)
právě když
=\left\{0\right\})
.
(d) Lineární zobrazení
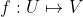
je prosté právě tehdy když libovolnou bázi
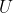
zobrazí na bázi
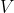
.