Zdravím
dokázal by tu niekto polopate vysvetliť toto lemma a jeho dôkaz
4. prednáška / Hladík
Ja som z toho tak najviac pochopil že by o platilo je potrebné Q=I
Edit
lemma znie ak A a B su regulárne v RREF
a Q je regulárne tak A=B
a eŠte by som poprosil A=B, či musia byť všetky čísla totožné alebo sa myslí že RREF vzniknutých matíc je totoŽný
Lemma A=QB => A=B
Základy lineární algebry (vektorové prostory, lineární zobrazení, řešení soustav lineárních rovnic, matice).
-
Tommassino
- Matfyz(ák|ačka) level I
- Příspěvky: 35
- Registrován: 10. 9. 2009 21:03
- Typ studia: Informatika Mgr.
Re: Lemma A=QB => A=B
Příspěvek od Tommassino »
myslim, ze ta lemma rika, ze kdyz je jedna matice rovna nejake jine po vynasobeni regularni matici, tak musi mit stejnou mnozinu reseni ~ ty matice reprezentuji stejnou soustavu rovnic, mozna by to melo byt ne A=B ale neco jako 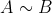 nevim jak se neco takoveho znaci xD
nevim jak se neco takoveho znaci xD
na dukaz se koukni sem http://www.karlin.mff.cuni.cz/~tuma/2003/NNLinalg3.pdf tvrzeni 3.13.1,3 a 4
ale nevim, mozna se pletu a ty myslis nejakou jinou lemmu
na dukaz se koukni sem http://www.karlin.mff.cuni.cz/~tuma/2003/NNLinalg3.pdf tvrzeni 3.13.1,3 a 4
ale nevim, mozna se pletu a ty myslis nejakou jinou lemmu
Zpět na „MAI057 Lineární algebra I“
Přejít na
- Aktuální informace
- ↳ Studijní oddělení
- ↳ Knihovna
- ↳ Studentská komora Akademického senátu (SKAS)
- ↳ Volby na ak. rok 2013/2014
- Všichni
- ↳ Práce
- ↳ Klubovna
- ↳ Toto fórum
- ↳ Státní závěrečná zkouška
- ↳ Bakalářské SZZ
- ↳ Magisterské SZZ
- ↳ Info for foreign students
- ↳ Akce
- ↳ Fotbalový turnaj 2008
- Informatika ZS
- ↳ Výuka ZS 1. ročník
- ↳ DMI002 Diskrétní matematika
- ↳ 2007
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ MAI054 Matematická analýza I
- ↳ 2007
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ MAI057 Lineární algebra I
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ PRG030 Programování I
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ SWI120 Principy počítačů a operačních systémů
- ↳ SWI087 Principy počítačů
- ↳ Ostatní
- ↳ DMI051 Úvod do řešení problémů kombinatorických, mat. i jiných (IPS) II
- ↳ Výuka ZS 2. ročník
- ↳ MAI056 Matematická analýza III
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ OFY016 Fyzika pro nefyziky I - Svět kolem nás
- ↳ SWI089 Ochrana informace I
- ↳ SWI096 Internet
- ↳ TIN061 Algoritmy a datové struktury II
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ Ostatní
- ↳ Aplikační software
- ↳ NPRG035 Jazyk C# a platforma .NET
- ↳ NPRG041 Programování v C++
- ↳ AIL062 Výroková a predikátová logika
- ↳ 2007
- ↳ 2006
- ↳ 2005
- ↳ PGR013 Java
- ↳ MAI059 Pravděpodobnost a statistika
- ↳ Výuka ZS 3. ročník
- ↳ SWI099 Administrace Systemu Windows
- ↳ SWI015 Programování v Unixu
- ↳ SWI098 Principy překladačů
- ↳ 2006
- ↳ Ostatní
- ↳ DBI007 Organizace a zpracování dat I
- ↳ 2006
- ↳ MAI062 Algebra I
- ↳ PGR003 Počítačová grafika I
- ↳ SWI090 Počítačové sítě I
- ↳ Výuka ZS NMgr.
- ↳ TIN066 Datové struktury I
- ↳ TIN062 Složitost I
- ↳ TIN064 Vyčíslitelnost I
- ↳ MAI060 Pravděpodobnostní metody
- ↳ SWI004 Operační systémy
- ↳ SWI106 Administrace Unixu
- ↳ Ostatní
- ↳ NTIN090 Základy složitosti a vyčíslitelnosti
- ↳ OPT042 Programování s omezujícími podmínkami
- ↳ AIL002 Neuronové sítě
- ↳ AIL025 Evoluční algoritmy I
- ↳ AIL069 Umělá inteligence I
- ↳ NDBI001 Dotazovací jazyky I
- ↳ TIN070 Testování software
- ↳ NDBI027 Datové sklady a analytické metody pro Business Intelligence
- ↳ NDBI034 Vyhledávání multimediálního obsahu na webu
- ↳ NPRG023 Softwarový projekt
- Informatika LS
- ↳ Výuka LS 1. ročník
- ↳ MAI055 Matematická analýza II
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ MAI058 Lineární algebra II
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ PRG031 Programování II
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ TIN060 Algoritmy a datové struktury I
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ SWI095 Úvod do UNIXu
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ Ostatní
- ↳ Výuka LS 2. ročník
- ↳ SWI071 Ochrana informace II
- ↳ TIN071 Automaty a gramatiky
- ↳ PRG033 Ročníkový projekt - specifikace
- ↳ DMI011 Kombinatorika a grafy I
- ↳ DBI025 Databázové systémy
- ↳ Ostatní
- ↳ SWI036 Programování pro Windows I & II
- ↳ SWI096 Internet
- ↳ PRG005 Neprocedurální programování
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ NSWI143 Architektura počítačů
- ↳ Výuka LS 3. ročník
- ↳ Ostatní
- ↳ PGR004 Počítačová grafika II
- ↳ PRG036 Technologie XML
- ↳ SZZ026 Bakalářská práce
- ↳ PRG003 Metodika programování a filozofie programovacích jazyků
- ↳ MAI064 Matematické struktury
- ↳ MAI042 Numerická matematika
- ↳ SWI021 Počítačové sítě II
- ↳ SWI045 Rodina protokolů TCP/IP
- ↳ NPRG038 Pokročilé programování pro .NET
- ↳ Výuka LS NMgr.
- ↳ SWI109 Konstrukce překladačů
- ↳ NPRG042 Programování v paralelním prostředí
- ↳ SWI117 Technologie vývoje webových aplikací
- ↳ SWI026 Softwarové inženýrství
- ↳ MAI061 Metody matematické statistiky
- ↳ I1 Ostatní Teoretická informatika
- ↳ I2 Ostatní Softwarové systémy
- ↳ I3 Ostatní Matematická lingvistika
- ↳ I4 Ostatní Diskrétní modely a algoritmy
- ↳ AIL026 Evoluční algoritmy II
- ↳ AIL070 Umělá inteligence II
- ↳ NDBI010 Dokumentografické informační systémy
- ↳ NDBI023 Dobývání znalostí
- ↳ NDBI016 Transakce
- ↳ NDBI006 Dotazovací jazyky II
- ↳ NAIL029 Strojové učení
- Matematika
- ↳ Výuka LS 1. ročník
- ↳ Lineární algebra 2
- ↳ Programování 2
- ↳ Matematická analýza 1b
- ↳ Volitelné předměty
- ↳ Výuka LS 2. ročník
- ↳ Pravděpodobnost a statistika
- ↳ Teorie Míry a integrálu II
- ↳ Algebra II
- ↳ Matematická analýza 2b
- ↳ Ostatní
- ↳ Výuka LS 3. ročník
- ↳ Předměty numeriky
- ↳ Úvod do funcionální analýzy
- ↳ Funkcionální analýza I
- ↳ Vybrané partie z funkcionální analýzy
- ↳ Náhodné procesy 2
- ↳ Matematická statistika 2
- ↳ Teorie pravděpodobnosti 2
- ↳ Matematická ekonomie
- ↳ Ostatní
- ↳ LS - Předměty MMIB a pokročilé Algebry
- ↳ Všeobecná diskuse
- ↳ Počítačová algebra
- ↳ Teorie čísel a RSA
- ↳ Aplikovaná kryptografie II
- ↳ Standardy v kryptografii
- ↳ Kryptoanalytické útoky
- ↳ Aplikace bezpečnostních mechanismů
- ↳ Kvantové a DNA počítače
- ↳ Faktorizace velkých čísel
- ↳ Algebraická geometrie v kladné charakteristice
- ↳ Výuka ZS 1. ročník
- ↳ MAA001 Matematická analýza 1a
- ↳ PRM044 Programování I
- ↳ MAA079 Proseminář z kalkulu 1a
- ↳ DMA005 Diskrétní matematika
- ↳ ALG001 Lineární algebra a geometrie I
- ↳ Ostatní
- ↳ Volitelné předměty
- ↳ Výuka ZS 2. ročník
- ↳ MIB
- ↳ Matematická analýza 2a
- ↳ Teorie míry a integrálu
- ↳ Numerika
- ↳ Algebra
- ↳ Předměty finanční matematiky
- ↳ Ostatní
- ↳ Výuka ZS 3. ročník
- ↳ Matematická statistika
- ↳ Teorie pravděpodobnosti
- ↳ Náhodné procesy
- ↳ Optimalizace
- ↳ Předměty numeriky
- ↳ Předměty finanční matematiky
- ↳ Komplexní analýza
- ↳ Funcionální analýza
- ↳ Ostatní
- ↳ ZS - předměty MMIB a pokročilé Algebry
- ↳ Úvod do algebry
- ↳ Složitost pro kryptografii
- ↳ Samoopravné kódy
- ↳ Teoretická kryptografie
- ↳ Aplikovaná kryptografie I
- ↳ Datové a procesní modely
- ↳ Eliptické křivky
- ↳ Členění kryptografických standardů
- ↳ Kryptografické protokoly
- ↳ Úvod do teorie grup
- ↳ Právní aspekty zabezpečení dat
- ↳ Komutativní okruhy
- Fyzika ZS
- ↳ Výuka ZS 1. ročník
- ↳ OFY067 Fyzika v experimentech I
- ↳ MAF027 Lineární algebra I
- ↳ OFY021 Fyzika I (mechanika a molekulová fyzika)
- ↳ OFY056 Programování pro fyziky
- ↳ MAF033 Matematická analýza I
- Oborový mix aktuální
- ↳ Anglický jazyk
- ↳ Tělesná výchova
- ↳ Granty GAUK
- Odkazy
- ↳ Wiki
- ↳ SKAS
- ↳ Spolek Matfyzák
- Matematika Archiv
- ↳ Výuka LS 2006/2007 3. ročník
- ↳ Předměty numeriky
- ↳ Úvod do funcionální analýzy
- ↳ Náhodné procesy 2
- ↳ Matematická statistika 2
- ↳ Teorie pravděpodobnosti 2
- ↳ Matematická ekonomie
- ↳ Výuka LS 2006/2007 2. ročník
- ↳ Pravděpodobnost a statistika
- ↳ Teorie Míry a integrálu II
- ↳ Angličtina
- ↳ Algebra II
- ↳ Matematická analýza 2b
- ↳ Ostatní
- ↳ Výuka LS 2006/2007 1. ročník
- ↳ Volitelné předměty
- ↳ Lineární algebra 2
- ↳ Programování 2
- ↳ Matematická analýza 1b
- Zrušené předměty
- ↳ SWI087 Principy počítačů
- ↳ SWI120 Principy počítačů a operačních systémů
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ PRG029 Programování v C++
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ PRG032 Objektově orientované programování
- ↳ 2006
- ↳ 2005
- ↳ 2004
- ↳ SWI097 Základy operačních systémů
- ↳ NDBI003 Organizace a zpracování dat II
- Roztřídit (resty)
- ↳ Výuka ZS 2005/06 2. ročník
- ↳ Předměty informační bezpečnosti
- ↳ Předměty finanční matematiky
- ↳ Teorie míry a integrálu
- ↳ Numerika
- ↳ Algebra
- ↳ Analýza/kalkulus
- ↳ Matematika obecně
- ↳ Výuka LS 2005/06 2.ročník
- ↳ Základy matematického modelování
- ↳ Finanční management
- ↳ Úvod do optimalizace
- ↳ Numerika
- ↳ Kalkulus
- ↳ Angličtina
- ↳ Diferenciální geometrie
- ↳ Pravděpodobnost a statistika
- ↳ Teorie míry a integrálu II
- ↳ Algebra II
- ↳ Analýza 2b