od mathemage » 6. 6. 2011 22:28
mathemage píše:Skupina A
1. Zformulujte a dokazte vetu o Sylvestrove zakonu setrvacnosti. (8 b)
viz Rocky I az Rocky V popr. Rocky Balboa

mathemage píše:
2. (a) Sestrojte matici projekce do
^T)
, a najdete projekci vektoru
^T)
. (2 b)
Primocare:
^T)
nacpes do matice
)
. Z vety o projekci do
)
z prednasky je matice projekce
^{-1}A^T)
. Projekce jest
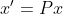
.
mathemage píše:
(b) Setrojte matici projekce do
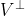
, a najdete projekci
vektoru x. (4 b).
^\bot = \mathcal{S}(A)^\bot = \mathcal{R}(A^T)^\bot = \textrm{Ker}(A^T))
. Naleznes reseni soustavy rovnic
)
, ta narves do matice B, a dale postupujes stejne jako v (2a).
mathemage píše:
3. Na ostrove Nova Guinea byl objeven novy druh zivocicha, nazvany
Commenticius Hladikensis:), se zvlastnim zivotnim cyklem. V prvnim roce po
narozeni jich prezije jen ctvrtina a v prumeru kazdy zplodi pul potomka. V
druhem roce kazdy zplodi v prumeru 2 potomky a uhyne.
(a) Bude populace zivocicha expandovat, ustali se, anebo vyhyne? (3 b)
! Pozor ! Hladikensis se dotycny rok vzdy nejdriv zpari (asi asexualne:) a teprve pak umre (tj. napr. v prumeru 1/2 potomka znamena kazdy zplodi 1/2 potomka a jen ctvrtina z nich tohle plozeni prezije:)
Vektor
^T)
, ten pronasobujes matici rekurence, tedy
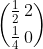
(zkus si to, odpovida to presne zadani). Postupne nasobeni touto matici odpovida vynasobeni jeji prislisnou vhodnou mocninou, takze vysetrujes, zda-li lim mocniny matice konverguje k 0, konverguje k nejakemu jinemu cislu ci diverguje. Mocnina "konverguje stejne jako" diagonalni matice z jeji diagonalizace, ktera ma na diagonale vl. cisla obou podobnych matic, tj. -1/2 a 1. Evidentne prvni dokonverguje k 0, to druhe je konstane 1, takze populace se ustali.
mathemage píše:
(b) Jaky je pomer jednotlivych vekovych populaci? (3 b)
Priznam se, ze az sem jsem se nedostal, ale rekl bych, ze proste napises soucin tech 3 matic z diagonalizace, ale ta prostredni diagonalni bude mit zminene limitni hodnoty. Tento soucin bude matice rekurence, ke ktere to vse konverguje, z te uz se pomer obyvatelstva urci pronasobenim se sloupcovym vektorem pocatecniho stavu (tj. pocet na zacatku, po prvnim roce). Asi, nevim, nevite nekdo lepsi reseni?
mathemage píše:
4. Rozhodnete a zduvodnete, ktera z nasledujich tvrzeni jsou pravdiva: (kazdy za 2 b)
(a) Existuje matice
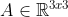
takova, ze
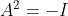
Tady nevim, mozna neco s vetou o odmocnine z matice - viz skripta
mathemage píše:
(b) Pro prostory U, V, W plati, ze pokud
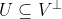
a
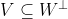
, potom
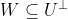
NE. Krkolomny protipriklad: Mej U, V a W podprostory nejakeho nenuloveho prostoru X. Vis, ze
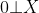
. Pro U := X & V := {0} & W := X. Pak nam plati
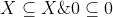
, ale pritom zjevne neplati
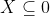
mathemage píše:
(c) Matice A =
6 pi 1 0 1
e 8 1 1 -3
-1 2 -9 3 2
2 0 e/pi 5 -1
1 2 1 -e 7
je regularni.
Typicka aplikace Gerschgorinovych disku, nesmi se ti v nich objevit 0 (aby nemohlo byt vl. cislem a tim i byt v soucinu vl. cisel, ktery se rovna determinantu, jenz je nenulovy jen a pouze pro regularni matice).
mathemage píše:
(d) Bud
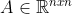
. Je-li
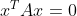
pro kazde
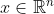
pak A = 0.
Nenech se osalit, nekoho by mohlo napadnout mluvit o PSD a rozkladu
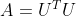
, ktery by povedl na ctverec normy vektoru Ux, jenz muze byt nulovy jen pro Ux=0 (neboli
 = \mathbb{R}^n)
, tedy
=\textrm{Ker}(U)^\bot = {0})
, tudiz radky jsou jen nulove vektory, takze U by melo byt 0-va matice a tim i A). For je ovsem v tom, ze A nemusi byt symetricka! Napr. A :=
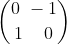
dava stejne hodnoty
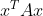
jako jeji zesymetrisovana verse
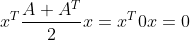
Prislo mi to tentokrat mnohem tezsi nez to, co bylo minuly tyden (tam byly priklady IMO primocarejsi, ted bylo tak nejak trosku vic vymysleni). Myslim, ze za jednicku celkove muzu byt jeste rad:)
[quote="mathemage"]Skupina A
1. Zformulujte a dokazte vetu o Sylvestrove zakonu setrvacnosti. (8 b)[/quote]
viz Rocky I az Rocky V popr. Rocky Balboa :D
[quote="mathemage"]
2. (a) Sestrojte matici projekce do [latex]V = span {(1,2,1)^T[/latex], a najdete projekci vektoru [latex]x = (1,1,0)^T[/latex]. (2 b)[/quote]
Primocare: [latex](1,2,1)^T[/latex] nacpes do matice [latex]A \in \mathbb{R}^{3x1} \Rightarrow V = \mathcal{S}(A)[/latex]. Z vety o projekci do [latex]\mathcal{S}(A)[/latex] z prednasky je matice projekce [latex]P = A(A^TA)^{-1}A^T[/latex]. Projekce jest [latex]x' = Px[/latex].
[quote="mathemage"]
(b) Setrojte matici projekce do [latex]V^\bot[/latex], a najdete projekci
vektoru x. (4 b).[/quote]
[latex]V^\bot = span{(1,2,1)^\bot = \mathcal{S}(A)^\bot = \mathcal{R}(A^T)^\bot = \textrm{Ker}(A^T)[/latex]. Naleznes reseni soustavy rovnic [latex](A^T |0)[/latex], ta narves do matice B, a dale postupujes stejne jako v (2a).
[quote="mathemage"]
3. Na ostrove Nova Guinea byl objeven novy druh zivocicha, nazvany
Commenticius Hladikensis:), se zvlastnim zivotnim cyklem. V prvnim roce po
narozeni jich prezije jen ctvrtina a v prumeru kazdy zplodi pul potomka. V
druhem roce kazdy zplodi v prumeru 2 potomky a uhyne.
(a) Bude populace zivocicha expandovat, ustali se, anebo vyhyne? (3 b)[/quote]
! Pozor ! Hladikensis se dotycny rok vzdy nejdriv zpari (asi asexualne:) a teprve pak umre (tj. napr. v prumeru 1/2 potomka znamena kazdy zplodi 1/2 potomka a jen ctvrtina z nich tohle plozeni prezije:)
Vektor [latex](\textrm{narozeni, prezivsi})^T[/latex], ten pronasobujes matici rekurence, tedy [latex]{\frac{1}{2}\,2 \choose \frac{1}{4}\,0}[/latex] (zkus si to, odpovida to presne zadani). Postupne nasobeni touto matici odpovida vynasobeni jeji prislisnou vhodnou mocninou, takze vysetrujes, zda-li lim mocniny matice konverguje k 0, konverguje k nejakemu jinemu cislu ci diverguje. Mocnina "konverguje stejne jako" diagonalni matice z jeji diagonalizace, ktera ma na diagonale vl. cisla obou podobnych matic, tj. -1/2 a 1. Evidentne prvni dokonverguje k 0, to druhe je konstane 1, takze populace se ustali.
[quote="mathemage"]
(b) Jaky je pomer jednotlivych vekovych populaci? (3 b)[/quote]
Priznam se, ze az sem jsem se nedostal, ale rekl bych, ze proste napises soucin tech 3 matic z diagonalizace, ale ta prostredni diagonalni bude mit zminene limitni hodnoty. Tento soucin bude matice rekurence, ke ktere to vse konverguje, z te uz se pomer obyvatelstva urci pronasobenim se sloupcovym vektorem pocatecniho stavu (tj. pocet na zacatku, po prvnim roce). Asi, nevim, nevite nekdo lepsi reseni?
[quote="mathemage"]
4. Rozhodnete a zduvodnete, ktera z nasledujich tvrzeni jsou pravdiva: (kazdy za 2 b)
(a) Existuje matice [latex]A \in \mathbb{R}^{3x3}[/latex] takova, ze [latex]A^2 = -I[/latex][/quote]
Tady nevim, mozna neco s vetou o odmocnine z matice - viz skripta
[quote="mathemage"]
(b) Pro prostory U, V, W plati, ze pokud [latex]U \subseteq V^\bot[/latex] a [latex]V \subseteq W^\bot[/latex], potom [latex]W \subseteq U^\bot[/latex][/quote]
NE. Krkolomny protipriklad: Mej U, V a W podprostory nejakeho nenuloveho prostoru X. Vis, ze [latex]{0} \bot X[/latex]. Pro U := X & V := {0} & W := X. Pak nam plati [latex]X \subseteq X \& {0} \subseteq {0}[/latex], ale pritom zjevne neplati [latex]X \subseteq 0[/latex]
[quote="mathemage"]
(c) Matice A =
6 pi 1 0 1
e 8 1 1 -3
-1 2 -9 3 2
2 0 e/pi 5 -1
1 2 1 -e 7
je regularni.[/quote]
Typicka aplikace Gerschgorinovych disku, nesmi se ti v nich objevit 0 (aby nemohlo byt vl. cislem a tim i byt v soucinu vl. cisel, ktery se rovna determinantu, jenz je nenulovy jen a pouze pro regularni matice).
[quote="mathemage"]
(d) Bud [latex]A \in \mathbb{R}^{nxn}[/latex]. Je-li [latex]x^TAx = 0[/latex] pro kazde [latex]x \in \mathbb{R}^n[/latex] pak A = 0.[/quote]
Nenech se osalit, nekoho by mohlo napadnout mluvit o PSD a rozkladu [latex]A = U^TU[/latex], ktery by povedl na ctverec normy vektoru Ux, jenz muze byt nulovy jen pro Ux=0 (neboli [latex]\textrm{Ker}(U) = \mathbb{R}^n[/latex], tedy [latex]\mathcal{R}(U)=\textrm{Ker}(U)^\bot = {0}[/latex], tudiz radky jsou jen nulove vektory, takze U by melo byt 0-va matice a tim i A). For je ovsem v tom, ze A nemusi byt symetricka! Napr. A := [latex]{0\,\,-1 \choose 1\,\,\,\,\,\,\,0}[/latex] dava stejne hodnoty [latex]x^TAx[/latex] jako jeji zesymetrisovana verse [latex]x^T\frac{A+A^T}{2}x = x^T0x = 0[/latex]
Prislo mi to tentokrat mnohem tezsi nez to, co bylo minuly tyden (tam byly priklady IMO primocarejsi, ted bylo tak nejak trosku vic vymysleni). Myslim, ze za jednicku celkove muzu byt jeste rad:)