od Tommassino » 27. 11. 2009 20:29
myslim, ze ta lemma rika, ze kdyz je jedna matice rovna nejake jine po vynasobeni regularni matici, tak musi mit stejnou mnozinu reseni ~ ty matice reprezentuji stejnou soustavu rovnic, mozna by to melo byt ne A=B ale neco jako
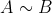
nevim jak se neco takoveho znaci xD
na dukaz se koukni sem
http://www.karlin.mff.cuni.cz/~tuma/2003/NNLinalg3.pdf tvrzeni 3.13.1,3 a 4
ale nevim, mozna se pletu a ty myslis nejakou jinou lemmu

myslim, ze ta lemma rika, ze kdyz je jedna matice rovna nejake jine po vynasobeni regularni matici, tak musi mit stejnou mnozinu reseni ~ ty matice reprezentuji stejnou soustavu rovnic, mozna by to melo byt ne A=B ale neco jako [latex]A\sim B[/latex] nevim jak se neco takoveho znaci xD
na dukaz se koukni sem http://www.karlin.mff.cuni.cz/~tuma/2003/NNLinalg3.pdf tvrzeni 3.13.1,3 a 4
ale nevim, mozna se pletu a ty myslis nejakou jinou lemmu ;)