Davpe píše:
14) Kolik je homomorfismu z grupy
)
do grupy
)
#homomorfismu ze
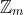
do
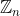
je NSD(m, n). Dukaz nepatri zrovna k tem nejtrivialnejsim, ale pokusim se o nej:
Zkoumejme, na jake podgrupy
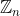
se muze homomorfismus

zobrazit (tj. velikost obrazu, oznacme ji

):
1)
 \leq \mathbb{Z}_n)
, tj.

deli

2)
 \simeq \mathbb{Z}_m/Ker f)
, jejiz velikost je index
![[\mathbb{Z}_m:Ker f]](http://latex.codecogs.com/gif.latex?[\mathbb{Z}_m:Ker f])
, ktery je z Lagrangeovy vety delitel radu grupy
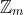
, neboli

deli take

Tudiz

deli i NSD(m, n). (jinymi slovy: Muzem tedy homomorfismem zobrazovat jen na podgrupu radu spolecneho delitele m a n).
Jak konkretne? Budeme zobrazovat

(generator v
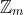
) na nejaky generator podgrupy (grupy
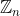
) vhodne velikosti r. Zbyvajici prvky jsou jasne dane, tj.
:= k f(1))
Ale kolik takovych generatoru je? - Presne jich je:
} \varphi(r))
coz se uplnou nahodickou i rovna NSD(m,n).
To se dokaze pocitanim 2 zpusoby: spocitame vsechny prvky
})
(1) trivialne je to NSD(m,n)
(2) kazdy prvek generuje prave 1 podgrupu nejake velikosti r, a ta je delitelem NSD(m, n) (dokonce podgrupa teto velikosti je prave 1!!). Tenhle prvek je generatorem teto podgrupy (a zadne dalsi), takze prispeje prave jednou

do (prave jedne) Eulerovy funkce
)
. V Eulorove funkci je prave jedna

za kazdy generator a nic dalsiho, a velikosti podgrupy (v sume jsou to ty "r") jsou prave jen delitele NSD a nic dalsiho.
shrnuto: #homomorfismu = #moznosti zobrazeni

na generator podgrupy vhodne velikosti r (viz vyse) = #takovych generatoru = NSD(m, n)
Q.E.D.
BTW nemate nekdo napad, jak jednodusejc to dokazat? Prijde mi, ze to urcite jde nejak zkratit/zjednodusit:)